ໃນການພິມເຜີຍແຜ່ນີ້, ພວກເຮົາຈະພິຈາລະນາຄໍານິຍາມ, ການຈັດປະເພດແລະຄຸນສົມບັດຂອງຫນຶ່ງໃນຮູບຮ່າງ geometric ຕົ້ນຕໍ - ສາມຫຼ່ຽມ. ພວກເຮົາຍັງຈະວິເຄາະຕົວຢ່າງຂອງການແກ້ໄຂບັນຫາເພື່ອລວບລວມເອກະສານທີ່ນໍາສະເຫນີ.
ຄໍານິຍາມຂອງສາມຫຼ່ຽມ
ສາມຫຼ່ຽມ - ນີ້ແມ່ນຮູບເລຂາຄະນິດຢູ່ໃນຍົນ, ປະກອບດ້ວຍສາມດ້ານ, ເຊິ່ງຖືກສ້າງຕັ້ງຂຶ້ນໂດຍການເຊື່ອມຕໍ່ສາມຈຸດທີ່ບໍ່ນອນຢູ່ໃນເສັ້ນຊື່ຫນຶ່ງ. ສັນຍາລັກພິເສດແມ່ນໃຊ້ສໍາລັບການກໍານົດ - △.
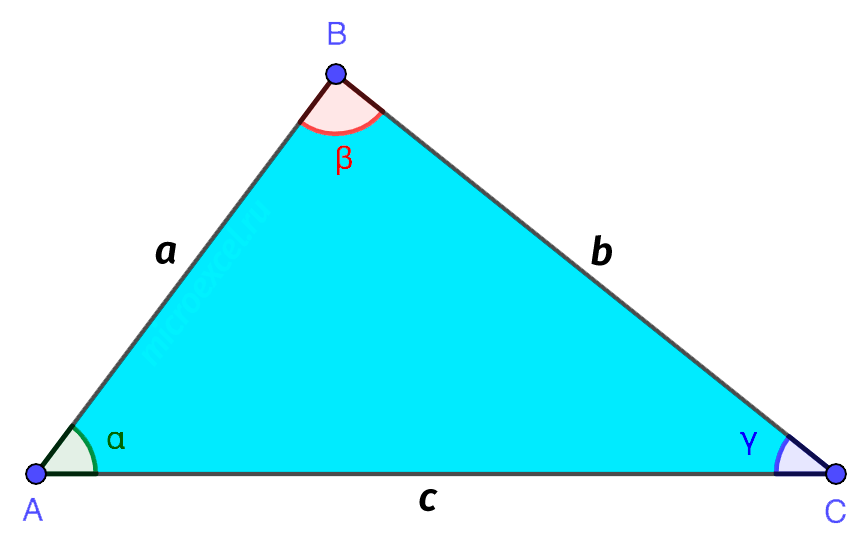
- ຈຸດ A, B ແລະ C ແມ່ນຈຸດຕັ້ງຂອງສາມຫຼ່ຽມ.
- ພາກສ່ວນ AB, BC ແລະ AC ແມ່ນດ້ານຂ້າງຂອງສາມຫຼ່ຽມ, ເຊິ່ງມັກຈະສະແດງເປັນຕົວອັກສອນລາຕິນໂຕດຽວ. ຕົວຢ່າງ, AB= a, BC = b, AND = c.
- ພາຍໃນຂອງສາມຫຼ່ຽມແມ່ນສ່ວນຂອງຍົນທີ່ຜູກມັດດ້ວຍສອງດ້ານຂອງສາມຫຼ່ຽມ.
ດ້ານຂ້າງຂອງສາມຫຼ່ຽມຢູ່ຈຸດຕັ້ງເປັນສາມມຸມ, ຕາມປະເພນີໝາຍເຖິງຕົວໜັງສືກເຣັກ - α, β, γ ແລະອື່ນໆ. ເນື່ອງຈາກວ່ານີ້, ສາມຫຼ່ຽມຍັງຖືກເອີ້ນວ່າ polygon ມີສາມແຈ.
ມຸມຍັງສາມາດສະແດງໄດ້ໂດຍໃຊ້ເຄື່ອງຫມາຍພິເສດ "∠"
- α – ∠BAC ຫຼື ∠CAB
- β – ∠ABC ຫຼື ∠CBA
- γ – ∠ACB ຫຼື ∠BCA
ການຈັດປະເພດສາມຫຼ່ຽມ
ອີງຕາມຂະຫນາດຂອງມຸມຫຼືຈໍານວນຂອງດ້ານເທົ່າທຽມກັນ, ປະເພດຂອງຕົວເລກດັ່ງຕໍ່ໄປນີ້ໄດ້ຖືກຈໍາແນກ:
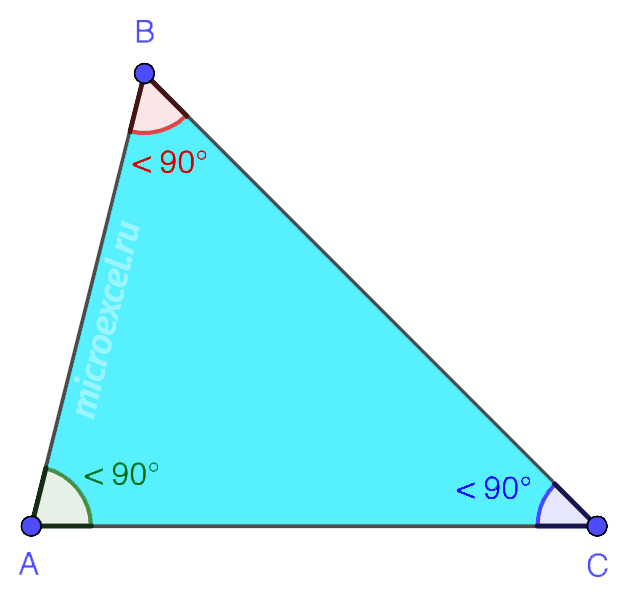
1. ມຸມສ້ວຍແຫຼມ – ສາມຫຼ່ຽມທີ່ມີທັງສາມມຸມສ້ວຍແຫຼມ, ເຊັ່ນ: ຫນ້ອຍກວ່າ 90°.
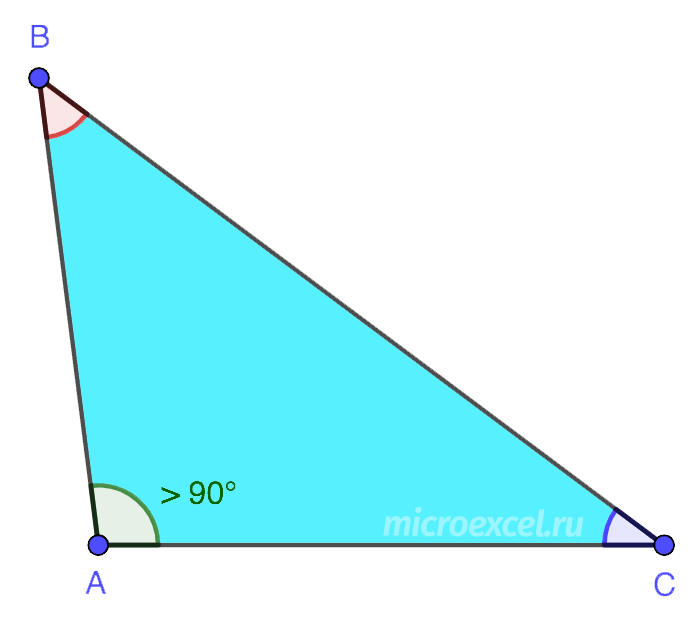
2. ສະຫຼຽງ ສາມຫຼ່ຽມທີ່ໜຶ່ງໃນມຸມໃຫຍ່ກວ່າ 90°. ອີກສອງມຸມແມ່ນສ້ວຍແຫຼມ.
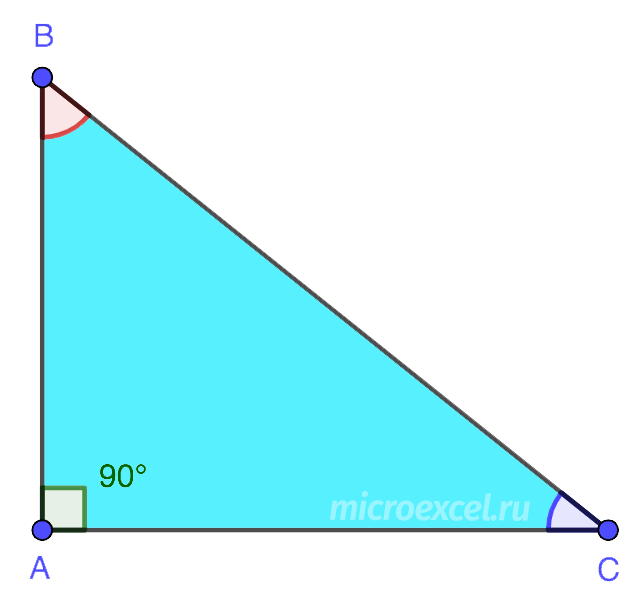
3. ມຸມສາກ – ສາມຫຼ່ຽມທີ່ມຸມໃດມຸມໜຶ່ງຖືກຕ້ອງ, ເຊັ່ນ: ເທົ່າກັບ 90°. ໃນຮູບດັ່ງກ່າວ, ສອງດ້ານທີ່ປະກອບເປັນມຸມຂວາເອີ້ນວ່າຂາ (AB ແລະ AC). ດ້ານທີສາມກົງກັນຂ້າມກັບມຸມຂວາແມ່ນ hypotenuse (BC).
4. versatile ສາມຫຼ່ຽມທີ່ທຸກດ້ານມີຄວາມຍາວແຕກຕ່າງກັນ.
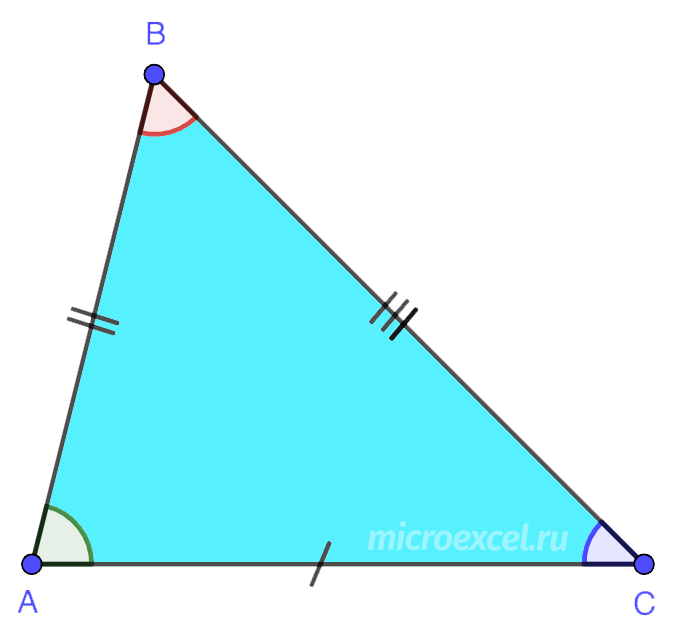
5. isosceles - ຮູບສາມຫຼ່ຽມທີ່ມີສອງດ້ານເທົ່າທຽມກັນ, ເຊິ່ງເອີ້ນວ່າຂ້າງ (AB ແລະ BC). ດ້ານທີສາມແມ່ນພື້ນຖານ (AC). ໃນຮູບນີ້, ມຸມພື້ນຖານແມ່ນເທົ່າທຽມກັນ (∠BAC = ∠BCA).
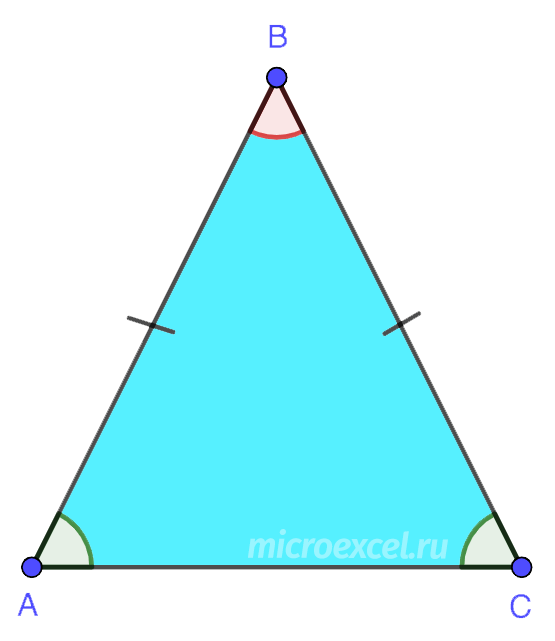
6. ເທົ່າກັນ (ຫຼືຖືກຕ້ອງ) ສາມຫຼ່ຽມທີ່ທຸກດ້ານມີຄວາມຍາວດຽວກັນ. ນອກຈາກນັ້ນ, ມຸມທັງຫມົດຂອງມັນແມ່ນ 60 °.
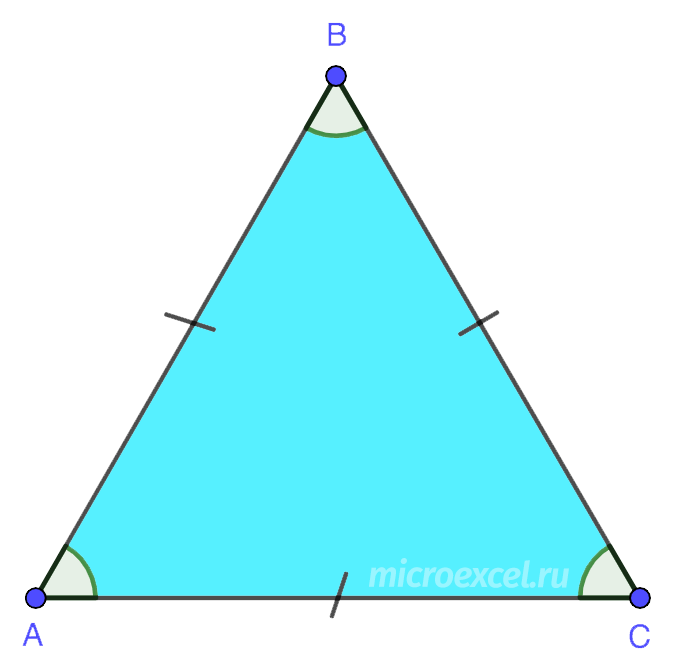
ຄຸນສົມບັດສາມຫຼ່ຽມ
1. ດ້ານໃດດ້ານໜຶ່ງຂອງສາມຫຼ່ຽມແມ່ນໜ້ອຍກວ່າອີກສອງດ້ານ, ແຕ່ໃຫຍ່ກວ່າຄວາມແຕກຕ່າງຂອງມັນ. ເພື່ອຄວາມສະດວກ, ພວກເຮົາຍອມຮັບການກໍານົດມາດຕະຖານຂອງສອງດ້ານ - a, b и с… ຈາກນັ້ນ:
b – c < a < b + cAt b > ຄ
ຄຸນສົມບັດນີ້ຖືກນໍາໃຊ້ເພື່ອທົດສອບພາກສ່ວນເສັ້ນເພື່ອເບິ່ງວ່າພວກເຂົາສາມາດສ້າງເປັນສາມຫຼ່ຽມໄດ້.
2. ຜົນບວກຂອງມຸມຂອງສາມຫຼ່ຽມໃດນຶ່ງແມ່ນ 180°. ມັນປະຕິບັດຕາມຄຸນສົມບັດນີ້ວ່າໃນສາມຫຼ່ຽມມຸມເຫວີ, ສອງມຸມແມ່ນແຫຼມສະເຫມີ.
3. ໃນສາມຫຼ່ຽມໃດ, ມີມຸມທີ່ໃຫຍ່ກວ່າກົງກັນຂ້າມກັບດ້ານທີ່ໃຫຍ່ກວ່າ, ແລະໃນທາງກັບກັນ.
ຕົວຢ່າງຂອງວຽກງານ
ວຽກ 1
ມີສອງມຸມທີ່ຮູ້ຈັກໃນສາມຫຼ່ຽມ, 32° ແລະ 56°. ຊອກຫາຄ່າຂອງມຸມທີສາມ.
ການແກ້ໄຂ
ໃຫ້ຂອງໃຊ້ເວລາມຸມທີ່ຮູ້ຈັກເປັນ α (32°) ແລະ β (56°), ແລະບໍ່ຮູ້ – ຢູ່ເບື້ອງຫຼັງ γ.
ອີງຕາມຊັບສິນກ່ຽວກັບຜົນລວມຂອງມຸມທັງຫມົດ, a + b + ຄ = 180 °.
ດ້ວຍເຫດນີ້, γ = 180° – ກ – ຂ = 180°–32°–56° = 92°.
ວຽກ 2
ໃຫ້ສາມສ່ວນຂອງຄວາມຍາວ 4, 8 ແລະ 11. ຊອກຫາວ່າພວກເຂົາສາມາດສ້າງເປັນສາມຫຼ່ຽມໄດ້.
ການແກ້ໄຂ
ໃຫ້ພວກເຮົາປະກອບຄວາມບໍ່ສະເຫມີພາບສໍາລັບແຕ່ລະພາກສ່ວນທີ່ລະບຸ, ໂດຍອີງໃສ່ຊັບສິນທີ່ໄດ້ກ່າວມາຂ້າງເທິງ:
11– 4 <8 < 11 + 4
8– 4 <11 < 8 + 4
11– 8 <4 < 11 + 8
ພວກມັນທັງໝົດແມ່ນຖືກຕ້ອງ, ດັ່ງນັ້ນ, ສ່ວນເຫຼົ່ານີ້ສາມາດເປັນດ້ານຂອງສາມຫຼ່ຽມໄດ້.










